A Drawer Contains 4 Pairs Of Blue Socks
A Drawer Contains 4 Pairs Of Blue Socks - We must pick a sock that is not a match to the first three. In how many ways can he do so?\n\\ ( \\begin {array} { l l l l } { \\text { (a) } 245 } & { \\text { (b) } 120 } & { \\text { (c) } 495 } & { \\text { (d) } 60. It feeds on fur, flannel, wool, soiled fabrics, and hair. If a drawer has 4 red socks and 4 blue socks a) if 2 are drawn what is the probability of a match? Calculate the probability that the maximum number of draws is required. Two socks drawn from the drawer will match if either both are brown or both are blue. Number of pairs of gray socks = 3. 4/9 out of 9 socks, 2 can be drawn in 9 c 2 ways. The probability of pulling out a brown sock at this point is 5 9, and the probability of pulling out a blue one is 4 9. A drawer contains 4 pairs of blue socks and 3 pairs of orange socks. If you randomly pick two socks, what is the probability that you obtain a matching pair? Web dressers & chests of drawers. Two socks are chosen at random without replacement. What is the probability that the second and third are also blue? Therefore, favorable number of cases is 5 c 2 + 4 c 2. (ii) assume again that the first selected sock is blue. Since we need to pick two socks, we can find the total number of all possible pairs of socks using combinations. We must pick a sock that is not a match to the first two. C) what is the probability of having all one color after 4 draws? If i. One sock at a time is randomly drawn from the drawer until a matching pair is obtained. In how many ways can 3 socks be selected such that both blue socks and green socks are selected? A drawer contains red, green, blue, and white socks with at least 2 of each color. We must pick a sock that is not. Total pairs of socks= 4 + 5 + 3 = 12. There are 6 socks left, and 4 of them are not a match. A drawer contains eight different pairs of socks. Therefore, favorable number of cases is 5 c 2 + 4 c 2. Two socks drawn from the drawer will match if either both are brown or both. Number of pairs of white socks = 5. There are 8 socks left in the drawer. The probability of pulling out a brown sock at this point is 5 9, and the probability of pulling out a blue one is 4 9. If you picked a red sock 4/6, if you picked another one it would be 3/5 as the. What is the probability that the second and third are also blue? To find the probability of picking two socks of the same color from the drawer, we can use permutations and combinations. Web a drawer contains 4 different pairs of socks. There are 6 socks left, and 4 of them are not a match. Therefore, favorable number of cases. If you picked a red sock 4/6, if you picked another one it would be 3/5 as the total number of socks has gone down as well as the number of red ones. What is the probability that the second and third are also blue? If you randomly pick two socks, what is the probability that you obtain a matching. The adult moths are very small and are rarely seen. 4/9 out of 9 socks, 2 can be drawn in 9 c 2 ways. Web a drawer contains four pairs of socks, with each pair a different color. P (pair)= [math processing error] answer link. Web a drawer contains 4 blue and 5 white socks. If i randomly pull 2 socks at the same time, what is the probability that the socks are the same color? If you randomly pick two socks, what is the probability that you obtain a matching pair? If a drawer has 4 red socks and 4 blue socks a) if 2 are drawn what is the probability of a match?. The pairs have been separated out and you must take out a pair of socks. Whether you’re looking for a traditionally styled bedroom dresser or modernly designed chest of drawers, ikea’s collection of affordable dressers features a host of options to perfectly match your space. But i do not know how to calculate the probability that the first two socks. Number of pairs of gray socks = 3. Differences are calculated from the matched or paired samples. Find the probability that (a) if 2 socks are selected at random they will form a pair, (b) if 4 socks are selected at random they will form 2 pairs. He has\nto select 4 socks from this set. Web my drawer contains 4 blue socks, 7 red socks, and 3 yellow socks. We must pick a sock that is not a match to the first two. In how many ways can he do so?\n\\ ( \\begin {array} { l l l l } { \\text { (a) } 245 } & { \\text { (b) } 120 } & { \\text { (c) } 495 } & { \\text { (d) } 60. I know that the probability that the first sock is blue is $\frac4{14}=\frac27 $. 4 white, 3 blue, and 5 grey. Total pairs of socks= 4 + 5 + 3 = 12. The pairs have been separated out and you must take out a pair of socks. If a brown sock is pulled out and not replaced: It feeds on fur, flannel, wool, soiled fabrics, and hair. A drawer contains red, green, blue, and white socks with at least 2 of each color. 4 are brown and 4 are blue. 4/9 out of 9 socks, 2 can be drawn in 9 c 2 ways.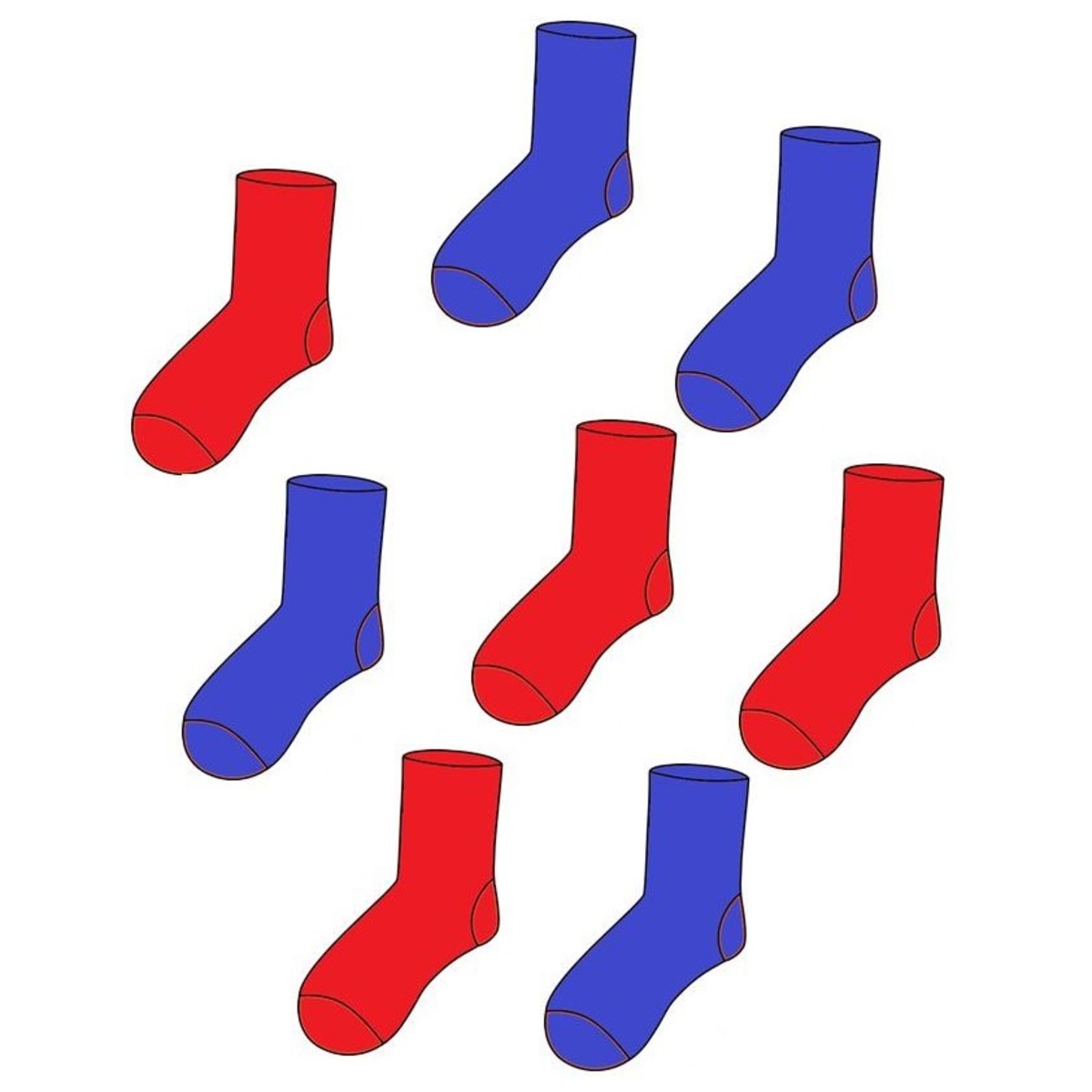
How Many Socks Make a Pair? A Mathematics Problem Owlcation

Drawer in the Closet for Storing Underwear, Socks and Bras. Vertical

SOLUTION A drawer contains 4 red socks, 6 white socks, and 10 blue
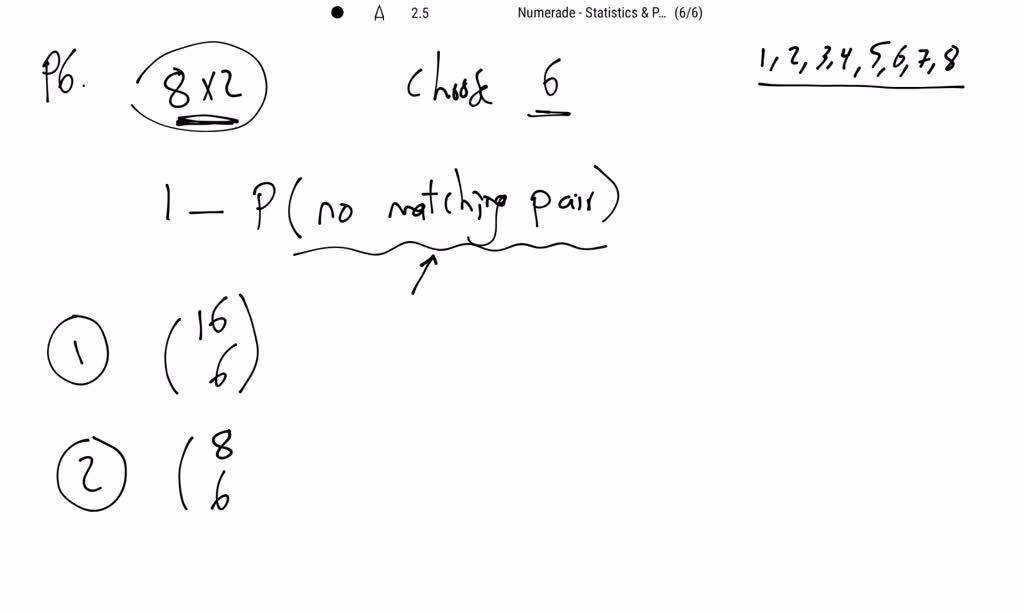
SOLVEDA drawer contains eight different pairs of socks. If six socks
PJKnits I Gotta Sock Drawer!

How to Organize Your Sock Drawer Martha Stewart YouTube

Pin by Yogita Salaskar on clothes to make Socks organizer, Diy sock
Solved A drawer contains 2 blue, 4 red, and 2 yellow socks.

15 Clever Sock Storage Ideas You'll Want to Try Sponge Hacks
MS. Simplicity Organize Your Socks And Underwear
What Is The Minimum Number Of Socks That Must Be Pulled From The Drawer To Guarantee A Matching Pair?
The Probability Of Pulling Out A Brown Sock At This Point Is 5 9, And The Probability Of Pulling Out A Blue One Is 4 9.
P (Rr)=4/6Xx3/5=12/30 If You Picked A Blue Sock 2/6, If You Picked Another One It.
I Solved (A) By Saying The Number Of Different Selections Of Socks Is (82) = 28 ( 8 2) = 28 Number Of Different Matching Combinations = 4
Related Post:
