How To Draw A Derivative
How To Draw A Derivative - Sketching a derivative using a function use the following graph of [latex]f(x)[/latex] to sketch a graph of [latex]f^{\prime}(x)[/latex]. Web figure 4.4.10 :the function f has a local maximum at x = − √3 and a local minimum at x = √3. A continuous function f has a local maximum at point c if and only if f switches from increasing to decreasing at point c. Where the slope is positive in the original, y’ is positive. A function f(x) is said to be differentiable at a if f ′ (a) exists. Web graphing of functions using first and second derivatives the following problems illustrate detailed graphing of functions of one variable using the first and second derivatives. It explains how to graph. First, notice that the derivative is equal to 0 when x = 0. Web courses on khan academy are always 100% free. We know from calculus that if the derivative is 0 at a point, then it is a critical value of the original function. A continuous function f has a local maximum at point c if and only if f switches from increasing to decreasing at point c. Read your original graph from left to right find any parabolic shapes or shapes where the curve looks flat. Web graphing of functions using first and second derivatives the following problems illustrate detailed graphing of functions. A continuous function f has a local maximum at point c if and only if f switches from increasing to decreasing at point c. When x < 0, x2 > 0 but (2x − 9) < 0, so f ′ (x) < 0 and the function is decreasing. Critical points (maximums and minimums) of the original equation are where the. The points c = 3, − 2 satisfy f ′ (c) = 0. Differentiation allows us to determine the change at a given. Web you just take the derivative of that function and plug the x coordinate of the given point into the derivative. Where the slope is positive in the original, y’ is positive. The derivative function, denoted by. Web courses on khan academy are always 100% free. We can use critical values to. That means the roots of f will. Web graphing of functions using first and second derivatives the following problems illustrate detailed graphing of functions of one variable using the first and second derivatives. Web sketching the derivative of a function. This relies on a solid understanding of functions, graphs, and the. Web general drawing rules of derivative f’ (x) 1. F ′ (x) = lim h → 0f(x + h) − f(x) h. It explains how to graph. Web about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features nfl sunday. First, we learn how to sketch the derivative graph of a continuous, differentiable function f (x), either given the original function or its graph y=f (x). Web general drawing rules of derivative f’ (x) 1. Let f be a function. Unleash the power of differential calculus in the desmos graphing calculator. A function f(x) is said to be differentiable at. When x < 0, x2 > 0 but (2x − 9) < 0, so f ′ (x) < 0 and the function is decreasing. At each point x, the derivative f ( x) < 0. Assuming that f is a polynomial, can i just pick the graphs of of f, f', and f'' visually by recalling that a derivative of. We can use critical values to. Web general drawing rules of derivative f’ (x) 1. Assuming that f is a polynomial, can i just pick the graphs of of f, f', and f'' visually by recalling that a derivative of a polynomial will produce an polynomial equation of a 1 lesser degree. Web thanks to all of you who support. Web evaluate derivatives, and draw the derivative function using the fx cg50. A function f(x) is said to be differentiable at a if f ′ (a) exists. So say we have f(x) = x^2 and we want to evaluate the derivative at point (2, 4). Critical points (maximums and minimums) of the original equation are where the zeros are now. Consider the function f(x) = x3 − (3 2)x2 − 18x. Differentiation allows us to determine the change at a given. Assuming that f is a polynomial, can i just pick the graphs of of f, f', and f'' visually by recalling that a derivative of a polynomial will produce an polynomial equation of a 1 lesser degree. Web these. Web these two critical points split the real line into 3 open intervals. Web evaluate derivatives, and draw the derivative function using the fx cg50. Sketching a derivative using a function use the following graph of [latex]f(x)[/latex] to sketch a graph of [latex]f^{\prime}(x)[/latex]. Web general drawing rules of derivative f’ (x) 1. Mark zeros at the locations of any turning points or stationary inflection points. This relies on a solid understanding of functions, graphs, and the. F ′ (x) = lim h → 0f(x + h) − f(x) h. ( − ∞, 0) (0, 9 / 2) (9 / 2, ∞) we need to determine the sign of the derivative in each intervals. Web thanks to all of you who support me on patreon. Web the derivative is zero where the function has a horizontal tangent. Web join subscribe subscribed share 170k views 5 years ago new calculus video playlist this calculus video tutorial provides a basic introduction into curve sketching. A function f(x) is said to be differentiable at a if f ′ (a) exists. Video tutorial w/ full lesson & detailed examples (video) Trust me, it’s straightforward, and you’ll get the hang of it in no time. Problems range in difficulty from average to challenging. Differentiation allows us to determine the change at a given.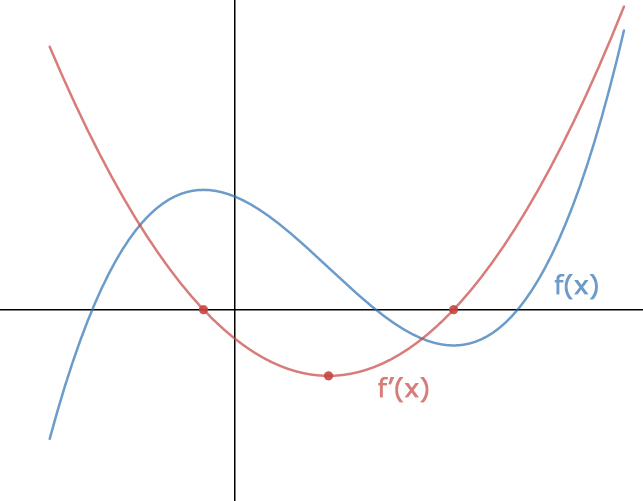
Sketching the Derivative of a Function Expii

Sketching the Derivative of a Function Expii

Sketching the graph of a derivative, (as in d𝑦/d𝑥), A Level Maths, 12th
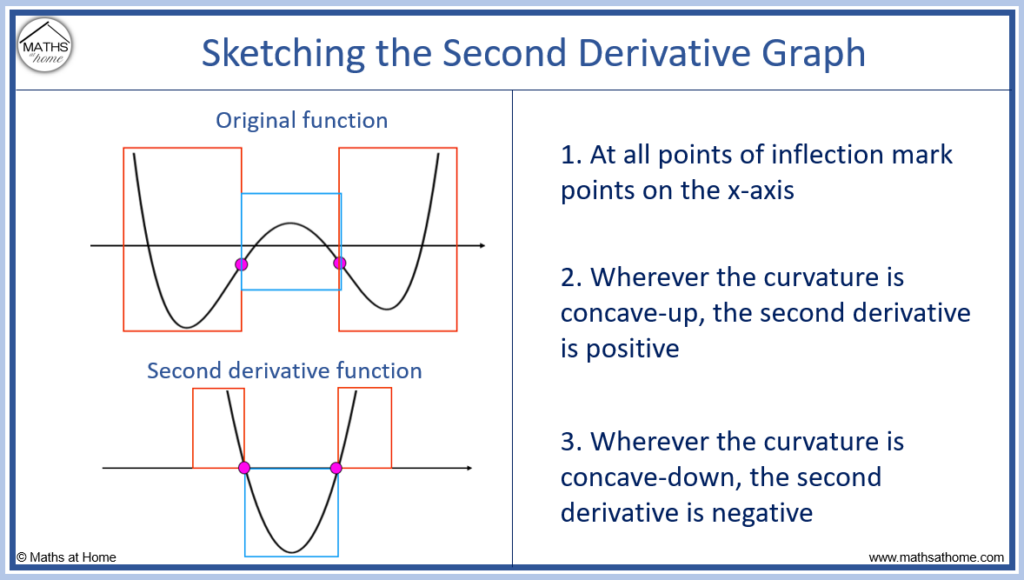
How to Sketch the Graph of the Derivative

Draw the Function given Graph of Derivative YouTube

Steps to Sketch Graph of Function From Derivative YouTube

How to sketch first derivative and Function from graph of second

MATH221 Lesson 009B Drawing Derivatives YouTube

Drawing the Graph of a Derivative YouTube
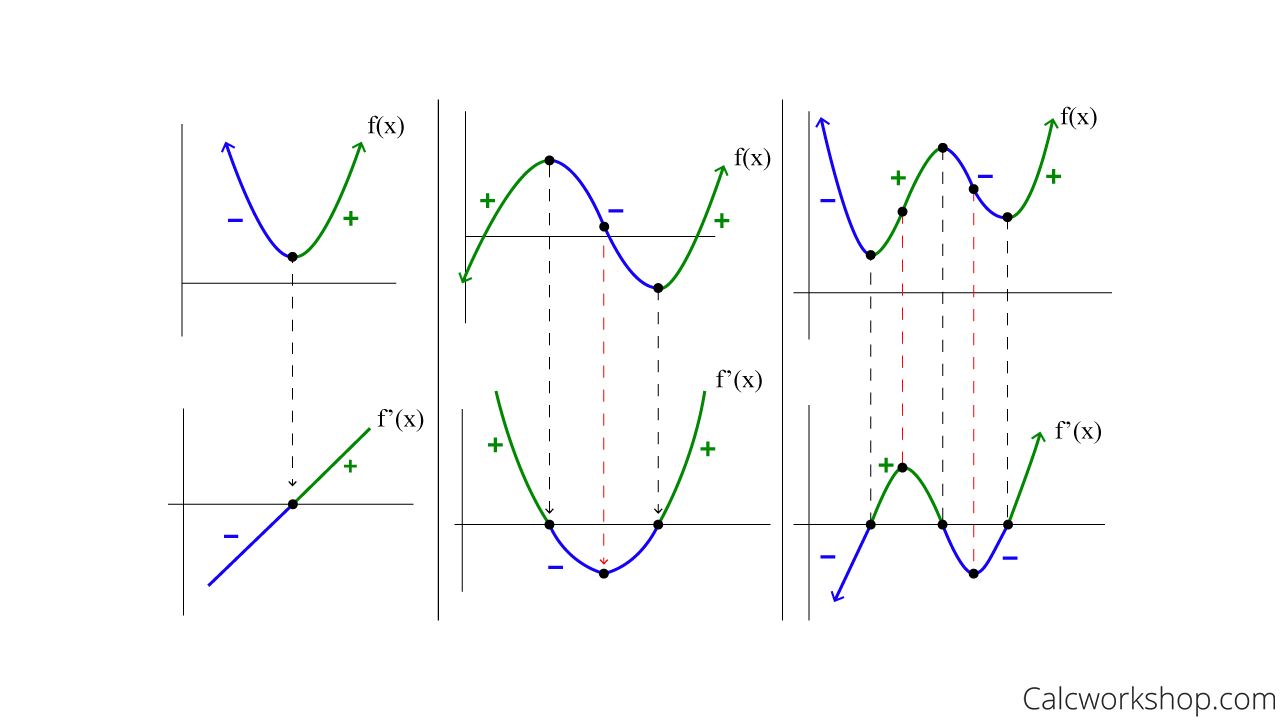
How To Sketch A Derivative Graph
It Explains How To Graph.
Web Sketching The Derivative Of A Function.
Web If The Original Graph Is Of A Parabola, Rather Than A Circle, Then The Graph Of The Derivative Is A Straight Line, Since D/Dx [Ax² + Bx + C] = 2Ax + B.
Web This Calculus Video Tutorial Explains How To Sketch The Derivatives Of The Parent Function Using The Graph F(X).
Related Post: